LeetCode: Merge Sorted Array Problem

The merge sorted array is one of the most popular problems on LeetCode specifically, and in coding interviews in general.

This article will explain the algorithm used to achieve the fastest, 0ms solution.

Description

Our job is to merge two arrays, nums1 and nums2. Thankfully, they are pre-sorted (phew, that makes our life easier!). We are also given two integers m and n, representing the number of elements in nums1 and nums2 respectively. What we actually need to do is merge nums1 and nums2 into a single array. But here's the catch - we need to do it in-place, meaning we have to put everything into nums1. No creating new arrays allowed!

The Solution

Instead of trying to shuffle elements around from the start (which would be a mess), we're going to work backwards. It's like playing Tetris in reverse - we start by placing the biggest numbers first!

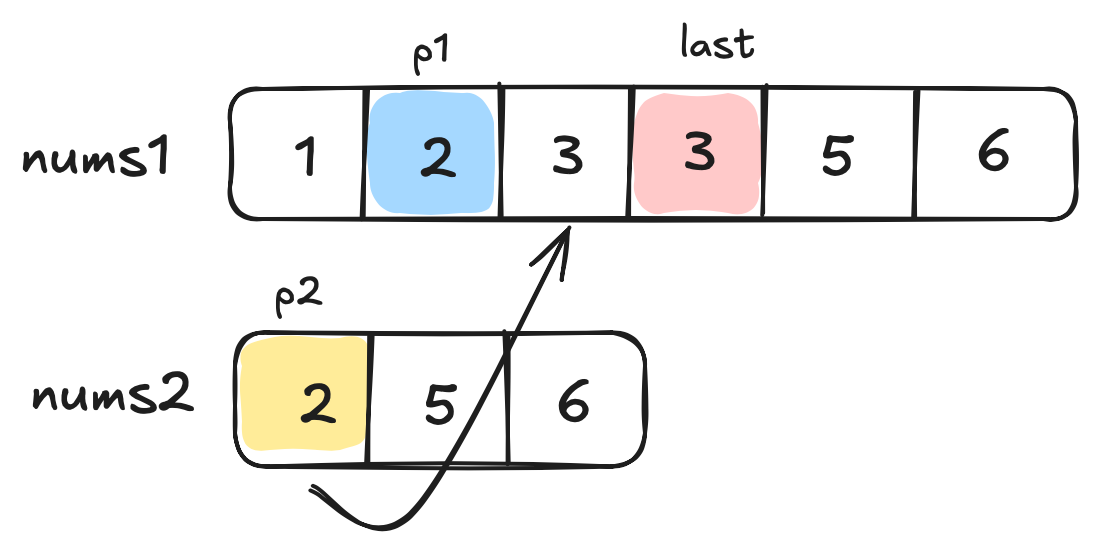
In this example we are given two arrays - nums1 contains the numbers [1,2,3] and 3 additional empty slots. nums2 contains the numers [2,5,6].

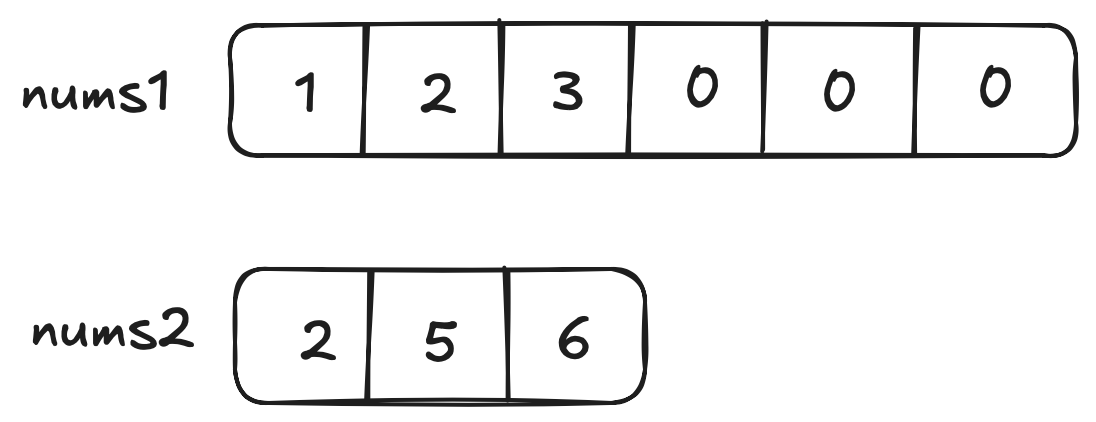
Here's how we do it:

1. First, we set up three pointers:

   • One at the last real number in nums1 (we'll call this p1)
   • One at the last number in nums2 (p2)
   • And one at the very end of nums1 where our final array will end (last)

2. Then, we play a game of "who's bigger?" Each time:

   • We compare the numbers at p1 and p2
   • The winner (bigger number) goes into the last position
   • We move the corresponding pointer and the last position marker back by one

The best part? No need to worry about shifting numbers around - we're filling the array from back to front!

Algorithm Walk-Through

We start by examining the last position of the merged array - position number 5 (which is identified in the code as the combination of m + n - 1). To fill in this position, we look in the last position of nums1 (p1) and the last position of nums2 (p2) and compare them. We find that number in the p2 position is bigger than the number in the p1 position. Great! So we fill in this number in the last position, and move up one step.

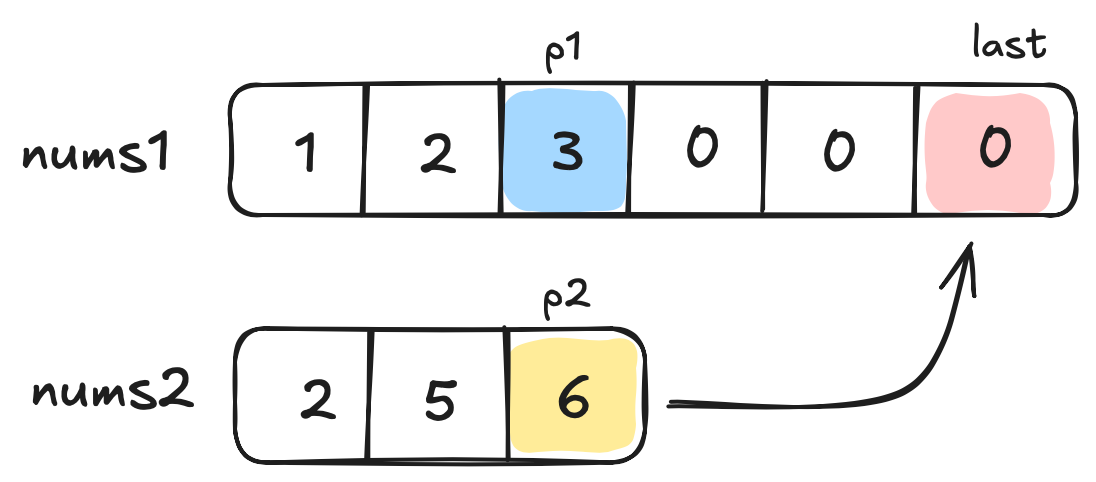To move up to this step, we actually move up the last position by one (since the previous one is already filled) and move p2 to the next position (since we've already made a decision on the previous member). We make the comparison again, and find that same as before, p2 > p1. We move up. 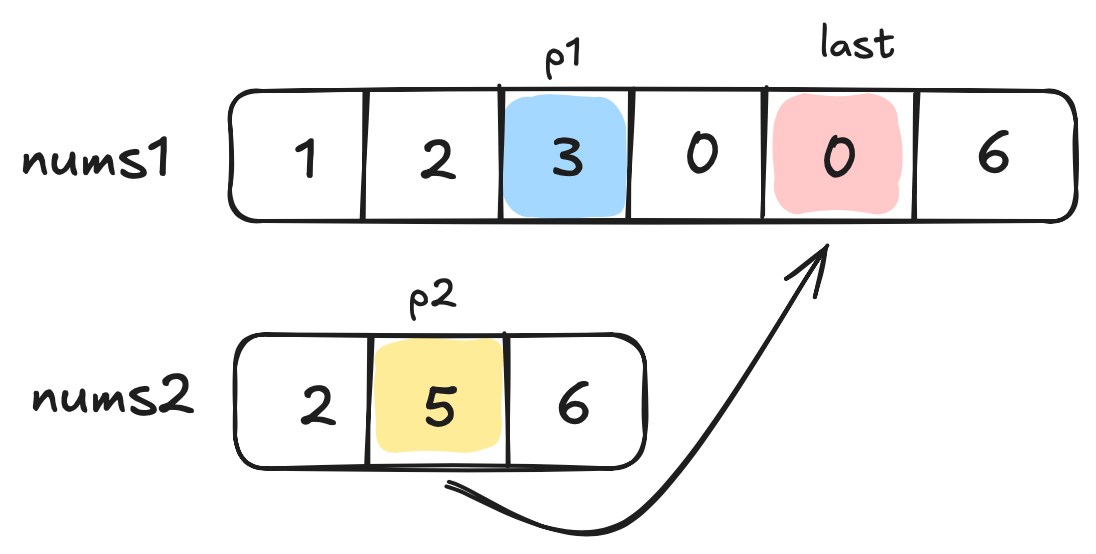In the next iteration - we find that p1 is actually bigger than p2 - so we fill up the new last position, and this time - we shift the p1 pointer - not p2.

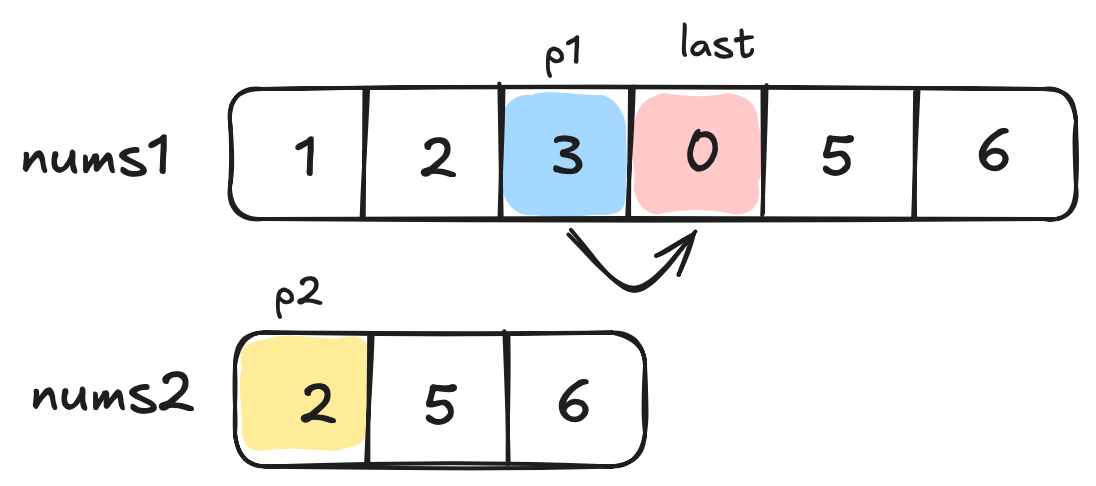
p2 > p1 - good. now we can again shift the last pointer and the p2 pointer. but oops - now p2 pointer location equals -1 - and that means the end of our comparison loop, since we have the merged array!

Here's the magic in Go code (with some helpful debug prints because who doesn't love seeing what's happening under the hood?)

func merge(nums1 []int, m int, nums2 []int, n int) {
    last := m + n - 1 // last index of merged array

    p1 := m - 1 // nums1 pointer to last nums1 index
    p2 := n - 1 // nums2 pointer to last nums2 index

    // if len(nums2) is smaller than 0, we don't need to iterate
    // we also need to make sure that nums1 is not empty
    for p2 >= 0 {
        fmt.Println("pointer p1:", p1)
        fmt.Println("pointer p2:", p2)
        // check if last member of nums1 larger than nums2
        if p1 >= 0 && nums1[p1] > nums2[p2] {
            // place nums1 member at the last index
            nums1[last] = nums1[p1]

            fmt.Println("nums1 after assignment:", nums1)
            // move pointer
            fmt.Println("moving p1")

            p1--
        } else {
            // place nums2 member at the last index
            nums1[last] = nums2[p2]

            fmt.Println("nums1 after assignment:", nums1)

            // move pointer
            fmt.Println("moving p2")
            p2--
        }
        // move last pointer
        fmt.Println("moving last")
        last--
    }
}

And that's it! No fancy algorithms, no complex data structures - just three pointers and some careful comparison logic. The best solutions are often the simplest ones, right? Remember: working backwards can sometimes be the way forward. In this case, it helps us avoid the headache of shifting elements around and gives us a clean, efficient solution. Happy coding! 🚀